Leverage Harvard’s OpenDP to run analytics with user-level differential privacy

This post comes with a Notebook to play with.

Since its formalization in Dwork, McSherry, Nissim and Smith’s 2006 seminal paper [1], differential privacy (DP) has gained tremendous traction among data privacy experts. Research on the subject receives increasing attention, and it has seen adoption by both industry leaders [2, 3, 4] and public institutions [5]. In order to develop usage, it is now necessary to make off-the-shelf and easy to use DP libraries widely available. A number of initiatives has been proposed for accounting [6], deep learning [7, 8] and basic building blocks [9, 10, 11].

Among those, Harvard’s OpenDP library proposes an intuitive way to build data analysis pipelines with privacy guarantees. A nice feature of the OpenDP framework is that, once a data pipeline has been written using their composable peer-reviewed primitives, the pipeline is guaranteed to be Differentially Private. You can check their tutorials for more information. In addition to the pre-built algorithms, it allows for easily customizable code and user-defined functions.

For example, let’s take a look at a sum aggregation of players’ score of some game (where the score belongs to [-10, 10]):

from opendp.transformations import *
from opendp.measurements import make_base_laplace
from opendp.mod import enable_features, binary_search_param
enable_features('contrib') # we are using un-vetted constructors
enable_features("floating-point")

dataset = """
  Cynthia,7
  Frank,5
  Frank,1
  Kobbi,8
  Kobbi,-8
  Kobbi,-6
  Kobbi,1
  Kobbi,-8
  Adam,-1
"""

num_tests = 5 # d_in=symmetric distance; this is public knowledge
budget = 50. # d_out=epsilon; in real use cases use a small epsilon
  # and many more rows (with 100 times more rows you
  # can divide the budget by 100)

bounds = (-10., 10.) # range of valid scores - public knowledge
constant = 0. # impute nullity with a guess

transformation = (
    make_split_dataframe(',', col_names=['Player', 'Score']) >>
    make_select_column(key='Score', TOA=str) >>
    make_cast(TIA=str, TOA=float) >>
    make_impute_constant(constant=constant) >>
    make_clamp(bounds) >>
    make_bounded_sum(bounds)
)

make_chain = lambda s: transformation >> make_base_laplace(s)
scale = binary_search_param(make_chain, d_in=num_tests, d_out=budget)
measurement = make_chain(scale)
release = measurement(dataset) # -> -0.8179450015793795

Here, we compute a DP-estimate of the sum of a column. To do so, we have to use some public knowledge: the maximum number of times a player appears in the dataset and the range of values. However, what happens if some of that information is missing ? For example, what if each player played a different number of game ? In our example, the number of game is necessary to compute the sensitivity of the query, which is a bound on how much can one player impact the result of the query: if we removed (or added) all the observations belonging to one player, it would change the result by at most 10 (the maximum absolute score) times the number of games.

Since this is exactly what DP wants to mitigate, we have to somehow set its value. If it’s not publicly known, we can estimate it using DP and clip the impact of each player on the sum result. However, increasing the sensitivity means increasing the noise added to the result. For a Laplace Mechanism, the added noise for a budget epsilon is:

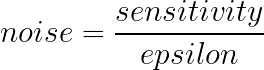
With that in mind, we see that we can’t just set the sensitivity to a high value that would encompass all players because it would introduce a larger than wanted variance. On the other hand, setting it too low means discarding some exams to forcefully reduce some players’ impact on the final result, which introduces bias. A tradeoff is necessary between bias and variance. Thankfully, some approaches have been proposed to find an acceptable value [12].

Here, let’s suppose we have a reasonable value s, but that some outlying players played an unexpected number of games higher than our sensitivity. We have to take it into account in our computation ! Currently, OpenDP doesn’t have this transform readily available, so let’s implement it.

Implementing a custom make_bounded_capped_sum()

We have to cap the importance of all players to a pre-determined value s. For players who appears less than s times, there is no problem. For those who appear N > s times, we can:

• sample s games among the N.
• add a s/N weighting factor so the influence of this player totals to s.

While the first solution works, it adds a random element to the process on top of DP that may not be welcome in most applications, so let’s focus on the second one.

We are going to add two preprocessing functions: one that groups observations by player, and one that takes as input a max_sensitivity parameter and compute a per_user sum while capping the sensitivity. To do so, we will use OpenDP’s make_default_user_transformation() transform.

make_default_user_transformation() takes as argument:

• a function defining the transform,
• a stability map that defines how the sensitivity is impacted by the transform,
• input and output domains specifying what kind of data is allowed in input and expected as output,
• input and output metrics defining how distances between datasets should be measured.

from opendp.combinators import make_default_user_transformation
from opendp.typing import *
import numpy as np
from json import loads, dumps
enable_features('honest-but-curious')


def make_groupby_user(users):
  users = np.array(users)
  return make_default_user_transformation(
    lambda x: [
      dumps((np.array(x)[users == user]).tolist()) for user in set(users)
    ],
    stability_map=lambda x: 1, # reset stability: one line == one user
    DI=VectorDomain[AllDomain[f64]],
    DO=VectorDomain[AllDomain[String]], # we can't use Vecs so we serialize
    MI=SymmetricDistance,
    MO=SymmetricDistance,
  )

def make_capped_user_sum(max_sensitivity):
    return make_default_user_transformation(
        lambda user: [
          min(  # weight sum by s/N if s < N
            1,
            max_sensitivity / len(loads(user_data))
          ) * sum(loads(user_data))
          for user_data in user
        ],
        stability_map=lambda x: x,
        DI=VectorDomain[AllDomain[String]],
        DO=VectorDomain[AllDomain[f64]],
        MI=SymmetricDistance,
        MO=SymmetricDistance,
    )

Putting it all together

Let’s see what we can get with our new function, without DP for now for a better comparison.

players = (
  make_split_dataframe(',', col_names=['Player', 'Score']) >>
  make_select_column(key='Player', TOA=str)
)(dataset)

sum_bounds = lambda max_sensitivity: (
  bounds[0] * max_sensitivity,
  bounds[1] * max_sensitivity,
)

transformation = lambda max_sensitivity: (
  make_split_dataframe(',', col_names=['Player', 'Score']) >>
  make_select_column(key='Score', TOA=str) >>
  make_cast(TIA=str, TOA=float) >>
  make_impute_constant(constant=constant) >>
  make_groupby_user(players) >>            # NEW!
  make_capped_user_sum(max_sensitivity) >>  # NEW!
  make_clamp(sum_bounds(max_sensitivity)) >>
  make_bounded_sum(sum_bounds(max_sensitivity))
)

print(transformation(5)(dataset))  # same as before
print(transformation(3)(dataset))  # Kobbi's importance is reduced by 2/5
print(transformation(1)(dataset))  # this is the sum of each player's mean

As we can see, reducing the sensitivity adds more bias: when its value is 3, player Kobbi’s games are weighted by 3/5 in order to get a sensitivity of 3. This is equivalent to removing its average mark twice to the total.

However, this also allows us to reduce the noise added by the Laplace Mechanism by 2/5. In our case, the error would change with the sensitivity this way:

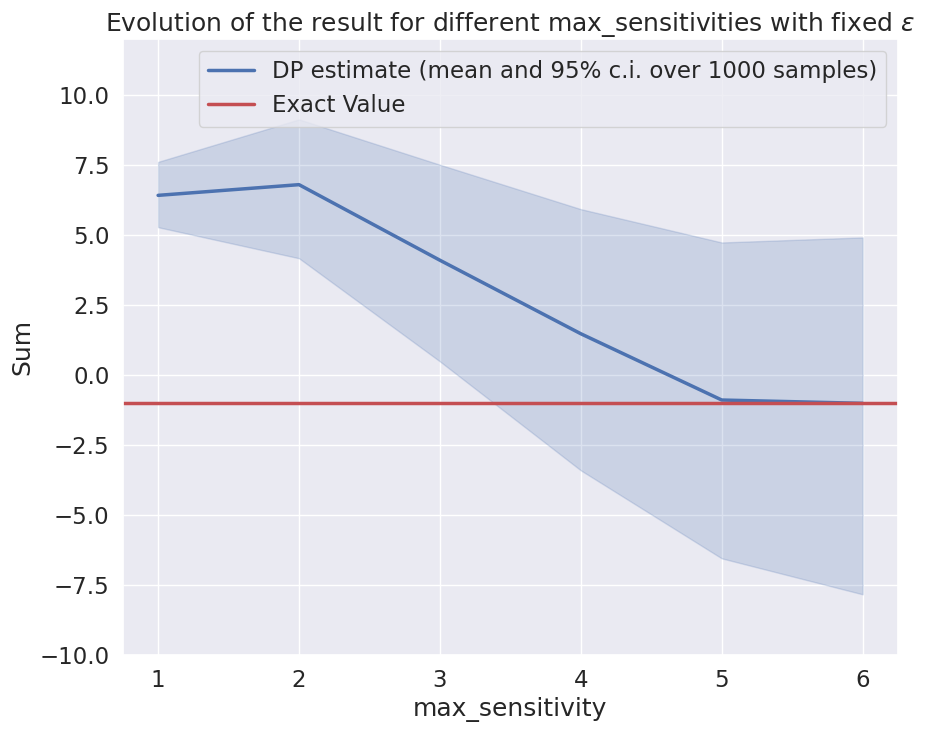
As we can see, when max_sensitivity is too high, the noise added makes the result unusable, but a value too low gives a result way too biased. Depending on what we want our analysis to achieve, we can set the right value to obtain the expected tradeoff.

Conclusion

In this blog post, we presented how to customize OpenDP’s functions so as to obtain guaranteed user-level privacy. The democratization of such tools might pave the way for a simpler and cheaper privacy protection at scale. At Sarus, we propose a solution allowing all data practitioners to analyze private data safely without having to know much about differential privacy and without changing too much their habits. For more information, please contact us.

References

[1] Dwork, C., McSherry, F., Nissim, K., & Smith, A. (2006). Calibrating noise to sensitivity in private data analysis. In Theory of Cryptography: Third Theory of Cryptography Conference, TCC 2006, New York, NY, USA, March 4–7, 2006. Proceedings 3 (pp. 265–284). Springer Berlin Heidelberg.

[2] Erlingsson, Ú., Pihur, V., & Korolova, A. (2014, November). Rappor: Randomized aggregatable privacy-preserving ordinal response. In Proceedings of the 2014 ACM SIGSAC conference on computer and communications security (pp. 1054–1067).

[3] Thakurta, A. G., Vyrros, A. H., Vaishampayan, U. S., Kapoor, G., Freudiger, J., Sridhar, V. R., & Davidson, D. (2017). Learning new words. Granted US Patents, 9594741.

[4] Ding, B., Kulkarni, J., & Yekhanin, S. (2017). Collecting telemetry data privately. Advances in Neural Information Processing Systems, 30.

[5] Abowd, J. M. (2018, July). The US Census Bureau adopts differential privacy. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (pp. 2867–2867).

[6] https://github.com/google/differential-privacy

[7] https://github.com/tensorflow/privacy

[8] https://github.com/pytorch/opacus

[9] https://github.com/IBM/differential-privacy-library

[10] https://github.com/OpenMined

[11] https://github.com/opendp/opendp

[12] Amin, K., Kulesza, A., Munoz, A., & Vassilvtiskii, S. (2019, May). Bounding user contributions: A bias-variance trade-off in differential privacy. In International Conference on Machine Learning (pp. 263–271). PMLR.

‍